結構前になりますが暗殺教室で体心立方格子の問題が出ていました。
中2の冬からアニメを見始めておよそ10年で
少なく見積もっても1000タイトル以上はアニメに費やしてしまった私は
いったい今何をしているかというとなぜか塾講師をしています。
ちなみに周りに言ったらよく驚かれるのですがマンガは見たことはありません。
(正確にはガンスリンガーガールというアニメが興味深く、
なんかのポイントがプレゼントされていたので
それを使って電子書籍としてマンガを購入したことはあります。)
話はそれましたが、
ある生徒が「クラスで頭のいい友達がいてこれ解けるか？って渡されたんですけど…」
といって手書きの問題を見せてくれました。
見たことある問題だったので「暗殺教室ですね。」と言いながらさらっとお話はしたのですが、
せっかくなら丁寧にやってあげたいと思い、
「急ぎでないなら時間いただけますか？」と言って次週
すみません、盛りました。ブログやりつつだったのでもう1週かかってしまいました…
堂々とA4で14枚、文字数にして7500(迷惑)をお渡ししたわけです!!
ということで、以下はそれをコピペし、部分的に修正したものです。
(コピペしたので「である調」のままで少しきつい言い方ですがご了承ください。)
「これでもか‼」というくらい分割して考えていますので
他の解説を読んで納得に至らない方も解決の糸口にはなると思いますので、
上から丁寧に読んでいってみてください。
画面構成上の関係で、先に問題の図を出します。
問題文の「右の図」は以下のものを参考にしてください。
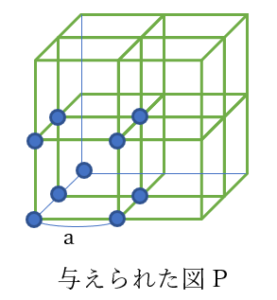
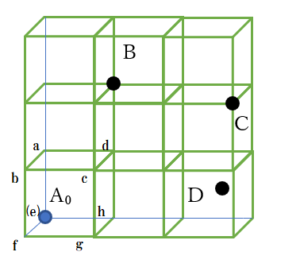
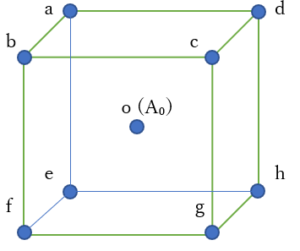
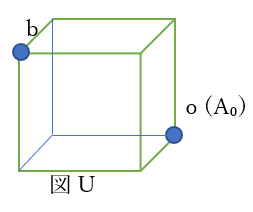
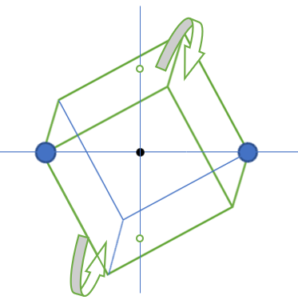
右の図のように1辺aの立方体が周期的に並びその各頂点と中心に原子が位置する結晶構造を体心立方格子構造という。NaやKなどのアルカリ金属の多くは体心立方格子構造をとる。体心立方格子構造においてある原子A₀に着目したとき、空間内のすべての点のうち、他のどの原子よりも A₀に近い点の集合がつくる領域をD₀とする。このときD₀の体積を求めよ。
＜図と体心立方格子構造の前提＞
高校化学で体心立方格子・面心立方格子・六方最密構造(充填)という
3つの結晶構造を最初の方でやる。
「結晶」とは簡単に言えばまったく同じ構造が規則的・周期的に続く構造のことを言う。
上の初期に与えられた図Pは立方体が8個集まった結晶構造に見える。
ただし、混同しないように最初に注意すると、あくまで「体心立方格子」とは
立方体の「中心１つ」と「頂点8つ」の結晶構造に与えられた名前なので、
図Pの左下に最初から記入された「1辺aの立方体にあたる構造体」が
体心立方格子と言える。
(しかし、結晶構造が周期的に繰り返す構造であることに注意すると
以下で出てくる図の点dにあたる部分から見ても体心立方格子であるとわかる。
ただの「体心立方格子」なのか「体心立方格子構造」なのかはきちんと理解する。
とは言っても、
「これ」と言われているのか
「これら」と言われているかの違い程度でしかないのであまり気にしなくてよい。)
※「体心立方格子(body-centered cubic lattice)」が長くて嫌ならbccと略してよい。
こうした結晶には繰り返しの最小単位となる構造が必ずあり、それを単位格子という。
ちなみにここでは関係ないが単位格子の1辺の長さのことを格子定数という。
また、この章を学んだ時に「充填率」という考え方を学ぶが
それがわかればもっと簡単にわかる(が、この問題に限っては逆に混乱するかもしれない)。
＜解答＞
問題文に「体心立方格子構造においてある原子A₀に着目したとき」とあるので
まずA₀がどういう選び方があるのかを考える。
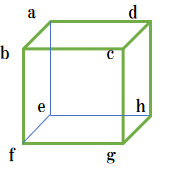
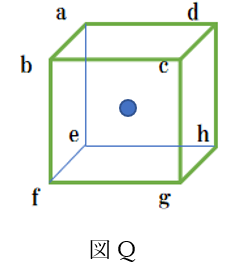
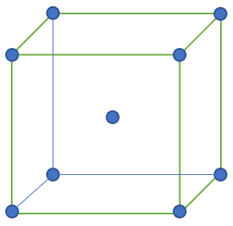
上の図は、図Pの左下にあった一辺aの単位格子の部分である。
頂点A₀の選び方は
① 中心の原子
② 8つの頂点のどれか
の9パターン(後述2パターン)にわけられる。
(頂点を原子A₀に選んだ時、他の頂点について考えてみると
相対的に位置関係のずれはない。もっと簡単に言えば
A₀を選んでから立方体をくるくる回転させると
結局他の頂点と一致するのでわざわざ場合をわけなくともよいということ。)
この図Pの左下の小立方体の頂点をそれぞれa~hまで名付ける。
問題は「D₀を求めること」だったのでそもそもD₀は何だったのかというところを見てみると、
「体心立方格子構造においてある原子A₀に着目したとき、
空間内のすべての点のうち、他のどの原子よりもA₀に近い点の集合がつくる領域」であった。
非常にわかりにくい。
分解して考える。
Ⅰ．「体心立方格子構造においてある原子A₀に着目したとき」
これは先ほど見た。中心か、それ以外(頂点)か。
Ⅱ．「空間内のすべての点のうち」
Ⅲ「他のどの原子よりもA₀に近い」
Ⅳ「点の集合がつくる領域」
Ⅱ．「空間内のすべての点のうち」
まず、Ⅱについて。「空間内」とはどこだろうか？
結晶構造が「周期的に並ぶ」ことが問題文でも言及されている。
つまり、初期に与えられた図Pのみを見ていると
考える世界がそこに限定されてしまう気がするが実際はもっとこの構造が続いている。
左図のように点BやCのようにとることもできるし、
空間内のすべての「点」(原子と言っていない)ので、点Dのようにとることもできる。
しかし直観的にもわかるように
頂点eを原子A₀に選んだとき
B,C,Dのように取るより前に頂点dや頂点hの方が「よりA₀に近そう」である。
つまりそんなに離れたところに目を向けなくてよいということである。
ここまでがⅡ．「空間内のすべての点のうち」にあたる。
Ⅲ「他のどの原子よりもA₀に近い」
Ⅲ「他のどの原子よりもA₀に近い」
に関しては上にあるⅡがわかれば同時解決できる人も多いかもしれない。
Ⅱまでで、「そんなに遠くまで考えなくてよい」ことがわかったところで、
「では、具体的にA₀に近い距離ってどこ？」
となったらここのステップにいる証拠である。
冒頭のA₀の選び方のところに関係する部分でもあるのでもう一度引用すると、
A₀の選び方は
① 中心の原子
② 8つの頂点のどれか
であった。
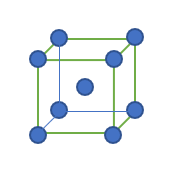
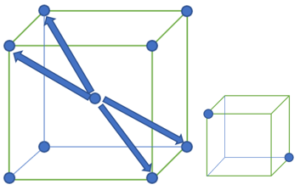
① に関して下図Qの中心原子をA₀として
Ⅲ「他のどの原子よりもA₀に近い」という文章をもう一回よく見てみると
“他のどの「原子」より”と書いてあるのがわかるだろうか。
体心立方格子の「中心」に位置する原子を基準に見れば
自然と最短距離にある「原子」は各頂点の原子だとわかる。
(しつこいけれどもここが重要)
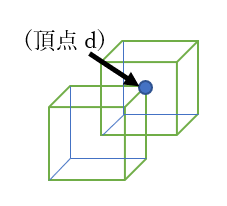
ところで、図Qを見てから頂点dを基準のA₀に選んだ時、最短距離になる
原子はどこになりそうか最初に予想してほしい。
以下、答えをすぐ出す。
頂点dをA₀としたときそもそも図Pでは8つの単位格子に分けられていたが
その各単位格子の中心の原子を結んだ時、
上図のように1辺の長さがaの
「dを中心とした体心立方格子」
ができることがわかるだろうか？
つまり、A₀の選び方は単位格子の頂点8つと中心原子1つの計9通りあり、
それを大きく分けると
① 中心の原子
② 頂点
の2通りに考え直すことができるが結局、
「中心をとっても頂点をとっても単位格子の中心の位置と変わらない
(中心原子の位置に帰着して考えられる)」ということである。
Ⅳ「点の集合がつくる領域」
最後にⅣ「点の集合がつくる領域」の意味解釈だが、
上のところまで理解してもここを誤解しやすい。
上の解釈で満足するとここを見落とすともいえるかもしれない。
「点」がつくる集合なのであり、その点が「原子」を指していないことに注意したい。
単位格子の各「頂点」を考えたばかりだったので「原子」
つまり立方体の頂点ばかり目が行ってしまうのも仕方ないが、
あくまで問われているのは領域。
どんな領域かと言えば、体積であり
その体積をつくるのは問題の指定によれば「点」ということをよく考える。
一度理解が進んだところで問題文を出すので読み直してほしい。
体心立方格子構造においてある原子A₀に着目したとき、空間内のすべての点のうち、他のどの原子よりもA₀に近い点の集合がつくる領域D₀を求めよ。
先ほどまでの前提より、A₀の選び方はどこを選んでも
結局「単位格子の中心と変わらない」とわかった。
そして求めるべきD₀は
「他のどの原子よりもA₀に近い点の集合」で構成されるのであった。
これらを踏まえると、D₀とは単位格子内で考えるべき領域だと推測できる。
<図形の基本性質について吟味する>
垂直二等分線について考える。
ここで言いたいことは「垂直二等分線が作図できる」とは全く違う能力の話である。
もちろん学校で垂直二等分線の「作図法」という技術的な話だけでなく、
「なぜ」そして「どういう理由」があり「そもそもどんな線なのか」を解説してくれた
良識ある先生に当たれば今から述べることは当たり前に知っているかもしれないが
ここの話はこの問題を解くうえで基礎となる考え方なので一応は目を通してほしい。
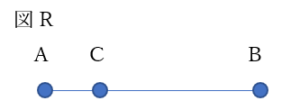
① 垂直二等分線はある2点から等しい距離にある「点」の集まりである
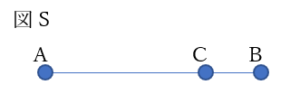
線分ABがあり、線分AB上に点Cを取ってみる。
図Rのようにとると点Aに近いことを直観的にわかる。
次に図Sのように点Cをとると点Bに近い。
そうしていくうちに点Aからも点Bからも等距離の点、点Cを決定できたとする。
これと同じことを今度は線分ABではないところにとっていく。
これを繰り返していくと下図のようになることが想像できる。
中学のカリキュラム上、相似や合同は作図を習った後でやる場合が多く
簡単な証明もできないため、こうした直観的に訴える方法しかとれないかもしれない。
しかし逆に言えば直観的にでも理解できれば
それで充分この体心立方格子の問題に取り組むことができる。
ここで取り上げたことで意識してほしいのは、
「ここで点をとると、点Aに近いよな～」
「でも、ここで点をとると逆に点Bに近くなってしまうよな～」
という試行錯誤をした感覚を頭の片隅に残しておきたいということである。
② 点対象な図形が対象の中心を通る線で面積を2等分する
こちらは解く上で必須ではないかもしれないが、
この視点が抜け落ちていると迷走してしまう人もいるかもしれないと考えたので
追加で記すことにした。
逆に、このことについて中学レベルで
一般的な点対象な図形全般について面積が等
分される証明が与えられることはなく、
性質として紹介されるのでその事実を知っている人はここをとばしてもよい。
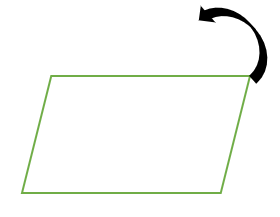
さて、簡単なモデルとして平行四辺形を考える。
まず一番最初の平行四辺形が基本の位置とする。
そして次の二番目の平行四辺形は少し左回りに回転させてみた図である。
最後にそのまま左へ回転させ続けた図が一番下の平行四辺形である。
平行四辺形のように図形の中心から
180度回転させて元の図形と一致するものを点対象な図形という。
そして回転の起点にした点を対象の中心という。
ざっくりしたイメージは、この平行四辺形の中心当たり
に画びょうを指して回すとき、その画びょうの位置が対象の中心である。
つまり1点だけ不動点を決めるということである。
そして、点対象な図形において対象の中心を通る線は面積を2等分する。
考えてみれば当たり前ではあるが、
点対象な図形とは対象の中心を起点に180度回転すると一致する図形、
つまり重なり合う図形のことであった。
なぜ点対象な図形が(対象の中心を通る線で)面積が2等分になるかの証明は
上でも述べたように通常与えられることはないが
回転とその意味を考えれば直観的に理解できる。
360度回転とは「寸分違わず元の場所に図の構成要素が戻ってくる」ことなので
当然に元の回転前の図形と一致する。
しかし、180度回転の場合は必ずしも一致するわけではない。
そしてその特別な場合、
つまり180度回転して一致する場合は対象の中心を通る線で面積が2等分される。
そして180度回転をもう一度続けて実行すると
180度×2で360度回転するので必ず回転前の図形と一致する。
ここまでのことを言い換えると
「当たり前に360度回転では一致するが、180度回転(半回転) でも一致する時
対象の中心を通る線で面積を2等分される」ということである。
180度(半回転)でも一致してしまう図形とはどういうことであろうか？
180度(半回転)でも一致してしまう図形
対象の中心を通る線を引いて2分した時にできた領域の片方にある図形が
180度回転したときの移転先にぴったり一致する形をしているからこそ
重なり合うということである。
これを別の表現で言えば、
同じ形でぴったり重なり合う図形とは、
それぞれの面積を比べた時面積が等しいといえる。
(面積が同じであっても同じ形かつ大きさであるとは必ずしも言えないが、
形が同じかつ大きさも同じ(＝合同)であれば面積は一致する。
上の例では「ぴったり重なり合う」ので形だけでなく大きさも同じ。)
<D₀とは実際にどんな領域か想像する>
重複するがD₀が単位格子内でできそうだとわかったので
もはや主人公は単位格子、つまり簡単な立方体に対して想像を巡らせることが正解への道である。
ということで、
<図T>
上の立方体<図T>は
単位格子を考え易くするために拡大した体心立方格子なので
図Pでいうところの左下の単位格子と同じというところは理解しておきたい。
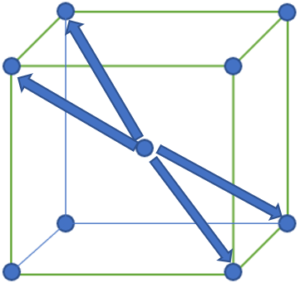
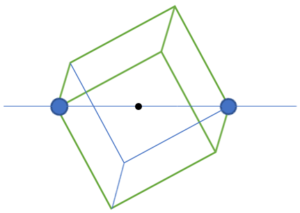
そして体心立方格子の中心oをA₀に選び頂点原子の位置との距離を比べる。
そしてこの直前の単位格子の図をよく見てみると、
「中心から頂点」という構造が8回あるので
この共通した構造に着目して、この単位格子を
さらに8つの小さな立方体に分けて考える。
(左の図では例として４頂点分示している)
「他のどの原子よりもA₀に近い点について」
問題文を再提示する。
「体心立方格子構造においてある原子A₀に着目したとき、空間内のすべての点のうち、他のどの原子よりもA₀に近い点の集合がつくる領域D₀を求めよ。」
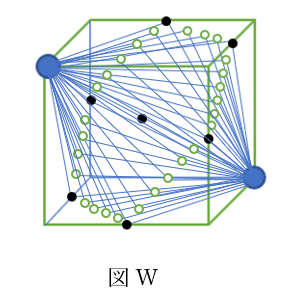
以下の図Uは
直前で出てきた単位格子を8つの立方体に分けたうちの
正面左上の小さな立方体を抜き出したものである。
図Uの点は上図Tの点bと点oにそれぞれ一致している。
点oをA₀と見たとき、もっとも近い「原子」は8つあり、
その基本的構造が一致しているのでモデルとして1つ
(ここでは単位格子正面左上の領域)を利用する。
このモデルのA₀から見て、
問題文の“他のどの「原子」よりも近い点”の
「原子」に当たる点は点bである。
2点bとoにおいてさらに簡略化して考えてみる。
まず最初のように「点」を考えるとよりA₀に近い。
「”他のどの原子”よりも近い点」について考えるので、
「A₀寄り」にとったこの点は領域D₀の構成要素であると言える。
そして次のような例をとると、
今度は逆に「他のどの原子」にあたる点ｂの方に近くなってしまう。
そうしているうちにちょうど「他のどの原子」よりも「A₀」よりも離れていない
つまり、「両端から等距離」である点を発見できたとする。
もうお気づきかもしれないが、この操作に覚えがあるはずである。
それは、上の章で出した垂直二等分線の考え方である。
※(「等距離」と「より」などに違和感をもつため問題に納得できない人がいるかもしれないが、
その場合は1/3=0.333...の感覚に頼ってみてほしい)
ここまで見てわかったように、
「他のどの原子よりも近い点」を考えるためには
「等距離の点」の集まりである垂直二等分線について考えれば
基準の両端(ここでは「他のどの原子」にあたる点ｂとA₀)から
等距離の点を図ることができるので、
「片方に寄りすぎない点」かつ「その限界」について知ることができる。
ただ、問題は平面ではなく立体なので、
「等距離の点」をすべて割り出すためには垂直二等分「面」について考える必要がある。
直観でどういう切り口になるかがわかる人はそれで良いが、
どうしてもわかりにくいという人もいると思うので、その手助けになるような思考を次に追加する。
わかる人は飛ばしてもよい。
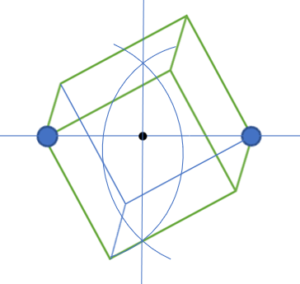
垂直二等分面によるアプローチ
結果としては、全12辺から原子部分に隣接する辺3本×2＝6本を引いた
6本(12－6＝6)の辺の各中点を通る面ができる。
これは正六角形になっている。
<垂直二等分面が想像できない人のための別のアプローチ>
まずは図Uの頂点ｂと頂点oを水平になるように持ちあげる。
そして、イメージとしては棒を点ｂ・中心・点oが一直線に突き抜けて串刺しにする。
※ここの「中心」は「点o」ではなく、単位格子の8分割した小立方の中心であり、
初めて出てきた「中心」なので混同しないように。
また忘れてはいけないのは
この中心が垂直二等分線によって作図された線分boとの交点であるということである。
つまり、
このような作図をもとに考えることができる点だということである。
そして、平面上ではこの直線はそもそも「両端点から等距離」の「点」が集まったものを
「線」として可視化したものであり、
逆に言えばこの線上のどこの1点を選んでも両端点までの距離が等しい。
これは、この線が「他のどの原子よりもA₀に近い点」の最終ラインになることを意味する。
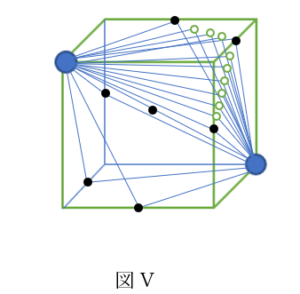
以下の図のように
作図に使った線は邪魔になるので垂直二等分線のみを残したものと、串刺しにした線を残す。
そしてこの二つを固定して立方体のみを回転させた様子を考える。
※立方体と棒を固定して(90度を維持しながら)垂直二等分線を動かしてもよい。
(しかし頭でやるなら後者は間違いやすいかもしれない。)
ちょうど串刺しにした線が軸となり垂直二等分線がナイフの役割をしているとき、
どのように切れるかを想像すると図Vと同じ軌跡をたどることが想像しやすいかと思う。
<領域D₀の体積>
領域D₀は単位格子内にできる領域であることは確認した。
単位格子は「中心」から「頂点」という構造が一致しているので
小立方体8つに分割して考えた。
そして分割した小立方体は2原子間で垂直二等分面の切断により
合同な2つの立体に分けられる。
※原子から切断面までの正六角錐と、
3つの合同な三角錐を合わせた立体が2つ合わさって小立方体になっている。
ここで逆算していくと、この最後に出てきた小立方体(図W)は
「他のどの原子よりもA₀に近い点の集合がつくる領域」を考えて
その結果が小立方体に正六角形の断面(境界面)として現れた図である。
そしてこの断面により合同な2つの立体に分けられた。
つまり、体積を2等分した。
またこの小立方体は単位格子の8分の１に当たる繰り返し構造であった。
ということは、
元の単位格子では“「中心」から「頂点」までを表した図W”と同じことが8回繰り返されるはず
なので、
「小立方体の体積が二等分されたうちの片方(A₀側)」×8＝D₀
となる。
直観的にD₀=a^3/2
でもよいが、一応丁寧に立式すると、
格子定数をaとし
{(a^3/8)*1/2}*8=D₀
左辺8を約分して、
a^3/2=D₀
追記
化学の厳密性と数学の図形問題としての見方によって、
それぞれ主張したいことが異なりやすい問題となっている。
問題文を一度再提示する。
右の図のように1辺aの立方体が周期的に並びその各頂点と中心に原子が位置する結晶構造を
体心立方格子構造という。NaやKなどのアルカリ金属の多くは体心立方格子構造をとる。体心立方格子構造においてある原子A₀に着目したとき、空間内のすべての点のうち、他のどの原子よりもA₀に近い点の集合がつくる領域をD₀とする。このときD₀の体積を求めよ。
この問題は、問題文の言い回しと定義不足のせいで解釈が難しくなっているだけである。
前半、原子や結晶構造の知識を持ち合わせている人は立方体の頂点部分を「点」ではなく
同じ半径の原子の並びを想像し、それらが接している様子
(充填率の問題でよく出てくる1/8球体×8個の立体)を想像してしまいやすい。
普通の解釈をする人は初見でこの問題を見たとき、
「空間内のすべての“点”」を各頂点の原子の部分と考えるのが普通だと思う。
原子＝点と解釈して読めばどこをA₀ととっても
問題文に周期性について言及されていることからも
D₀＝a^3と導くのが妥当である。
数学の集合論などで出てくる「領域」についても、
「点」の「集合」を「体積」と定義しているのもZ会監修と言えども奇問と言える。
どうしても「体心立方格子」という化学の知識を問題文にさらして、
複雑性を維持しつつ数学の問題として提示したいなら
点の定義を明確にするか、体心立方格子の説明の後、
「体心立方格子において原子が配置されるところに
数学的図形問題に帰着させるために格子点として点を再配置し、
原子の球体の概念を考慮する必要性をなくした。」
などとあくまで化学ではなく数学的な問題であると念を押すべきであろう。
